- Автор Abigail Brown [email protected].
- Public 2023-12-17 06:59.
- Последнее изменение 2025-01-24 12:22.
Регрессия в Excel - это способ автоматизировать статистический процесс сравнения нескольких наборов информации, чтобы увидеть, как изменения в независимых переменных влияют на изменения в зависимых переменных. Если вы когда-либо хотели найти корреляцию между двумя вещами, использование регрессионного анализа в Excel - один из лучших способов сделать это.
Инструкции в этой статье относятся к Excel 2019, Excel 2016, Excel 2013, Excel 2010.
В чем смысл регрессии?
Регрессия - это метод статистического моделирования, который аналитики используют для определения взаимосвязей между несколькими переменными.
Регрессионный анализ начинается с одной переменной, которую вы пытаетесь проанализировать, и независимых переменных, которые вы тестируете, чтобы увидеть, влияют ли они на эту единственную переменную. Анализ рассматривает изменения в независимых переменных и пытается сопоставить эти изменения с результирующими изменениями в единственной (зависимой) переменной.
Это может звучать как расширенная статистика, но Excel делает этот сложный анализ доступным для всех.
Выполнение линейной регрессии в Excel
Простейшей формой регрессионного анализа является линейная регрессия. Простая линейная регрессия рассматривает взаимосвязь только между двумя переменными.
Например, в следующей электронной таблице показаны данные, содержащие количество калорий, которые человек съедал каждый день, и его вес в этот день.
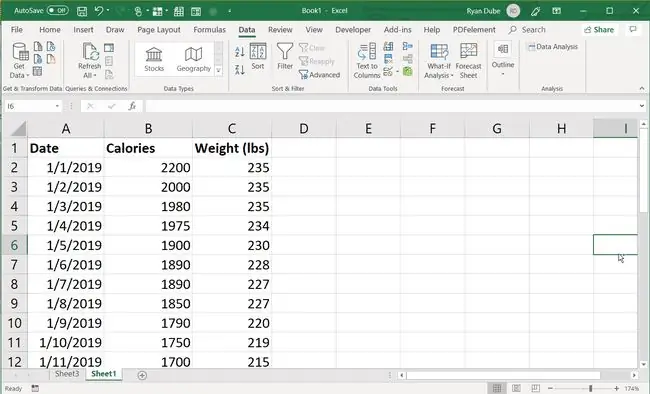
Поскольку эта электронная таблица содержит два столбца данных, и одна переменная потенциально может влиять на другую, вы можете провести регрессионный анализ этих данных с помощью Excel.
Включение надстройки Analysis ToolPak
Прежде чем вы сможете использовать функцию регрессионного анализа Excel, вам необходимо включить надстройку Analysis ToolPak на экране параметров Excel.
-
В Excel выберите меню Файл и выберите Опции.

Image -
Выберите Надстройки в левом меню навигации. Затем убедитесь, что Excel Add-ins выбрано в поле Управление.

Image -
Наконец, выберите кнопку Go.

Image -
Во всплывающем окне надстроек. Включите Analysis ToolPack, щелкнув поле перед ним, чтобы добавить галочку, и выберите OK..

Image
Теперь, когда пакет инструментов анализа включен, вы готовы приступить к выполнению регрессионного анализа в Excel.
Как выполнить простую линейную регрессию в Excel
Используя таблицу веса и калорий в качестве примера, вы можете выполнить линейный регрессионный анализ в Excel следующим образом.
-
Выберите меню Данные. Затем в группе Анализ выберите Анализ данных..

Image -
В окне Анализ данных выберите из списка Регрессия и нажмите OK.

Image -
Входной диапазон Y - это диапазон ячеек, который содержит зависимую переменную. В данном примере это вес. Input X Range - это диапазон ячеек, который содержит независимую переменную. В данном примере это столбец калорий.

Image -
Выберите Ярлыки для ячеек заголовков, а затем выберите Новый рабочий лист, чтобы отправить результаты на новый рабочий лист. Выберите OK, чтобы Excel выполнил анализ и отправил результаты на новый лист.

Image -
Изучите новый рабочий лист. Выходные данные анализа содержат ряд значений, которые необходимо понимать для интерпретации результатов.

Image Каждое из этих чисел имеет следующие значения:
- Multiple R: Коэффициент корреляции. 1 указывает на сильную корреляцию между двумя переменными, а -1 означает сильную отрицательную связь. 0 означает отсутствие корреляции.
- R Square: Коэффициент детерминации, который показывает, сколько точек между двумя переменными приходится на линию регрессии. Статистически это сумма квадратов отклонений от среднего значения.
- Скорректированный R-квадрат: статистическое значение, называемое R-квадратом, скорректированное с учетом количества выбранных вами независимых переменных.
- Стандартная ошибка: Насколько точны результаты регрессионного анализа. Если эта ошибка мала, то результаты вашей регрессии более точны.
- Observations: количество наблюдений в вашей регрессионной модели.
Остальные значения в выходных данных регрессии дают вам подробную информацию о более мелких компонентах в регрессионном анализе.
- df: Статистическая величина, известная как степень свободы, связанная с источниками дисперсии.
- SS: Сумма квадратов. Отношение остаточной суммы квадратов к общему SS должно быть меньше, если большая часть ваших данных соответствует линии регрессии.
- MS: средний квадрат данных регрессии.
- F: F-статистика (F-тест) для нулевой гипотезы. Это обеспечивает значимость регрессионной модели.
- Значимость F: статистическое значение, известное как P-значение F.
Если вы не разбираетесь в статистике и расчете регрессионных моделей, значения внизу сводки не будут иметь большого значения. Тем не менее, Multiple R и R Square являются двумя наиболее важными.
Как видите, в этом примере калории имеют сильную корреляцию с общим весом.
Множественный линейный регрессионный анализ в Excel
Чтобы выполнить ту же линейную регрессию, но с несколькими независимыми переменными, выберите весь диапазон (несколько столбцов и строк) для Input X Range.
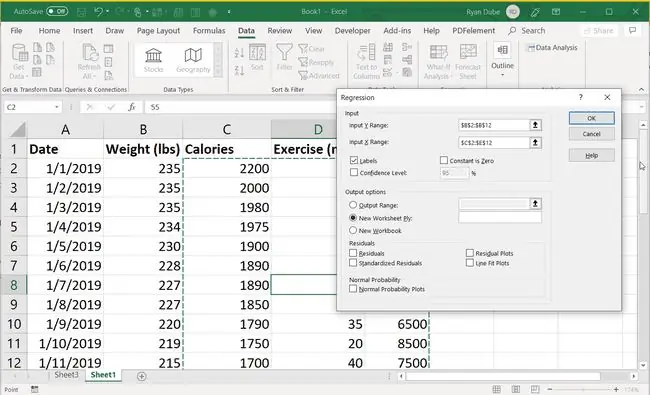
При выборе нескольких независимых переменных маловероятно, что вы обнаружите столь сильную корреляцию, потому что переменных очень много.
Однако регрессионный анализ в Excel может помочь вам найти корреляции с одной или несколькими из этих переменных, о существовании которых вы можете не подозревать, просто просматривая данные вручную.






